Compute a convex hull
Description:
The Problem
Consider a flat board with pegs sticking out of one side. If you stretched a rubber band across the outermost pegs what is the set of pegs such that all other pegs are contained within the shape formed by the rubber band?
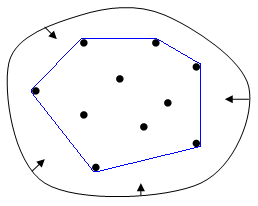
More specifically, for this kata you will be given a list of points represented as [x,y] co-ordinates. Your aim will be to return a sublist containing points that form the perimeter of a polygon that encloses all other points contained within the original list.
Notes:
The tests may include duplicate and/or co-linear points. Co-linear points are a set of points which fall on the same straight line. Neither should be included in your returned sublist
For simplicity, there will always be at least 3 points
Help:
Check out wikipedia's page on convex hulls
Note for python users: scipy module has been disabled.
Similar Kata:
Stats:
| Created | Nov 27, 2015 |
| Published | Dec 3, 2015 |
| Warriors Trained | 2691 |
| Total Skips | 956 |
| Total Code Submissions | 7021 |
| Total Times Completed | 439 |
| Python Completions | 301 |
| JavaScript Completions | 95 |
| Ruby Completions | 29 |
| Haskell Completions | 27 |
| Elixir Completions | 14 |
| Total Stars | 126 |
| % of votes with a positive feedback rating | 97% of 117 |
| Total "Very Satisfied" Votes | 112 |
| Total "Somewhat Satisfied" Votes | 4 |
| Total "Not Satisfied" Votes | 1 |
| Total Rank Assessments | 6 |
| Average Assessed Rank | 3 kyu |
| Highest Assessed Rank | 3 kyu |
| Lowest Assessed Rank | 5 kyu |