Earth-mover's distance
Description:
The earth-mover's distance is a measure of the dissimilarity of two probability distributions. The unusual name comes from thinking of the probability attached to an outcome x as a pile of dirt located at x. The two probability distributions are then regarded as two different ways of piling up a fixed amount of dirt over a region of space.
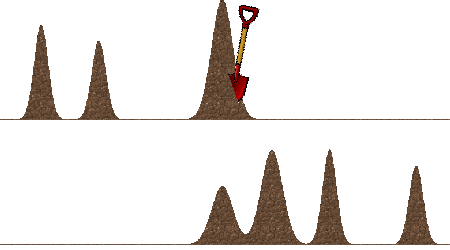
The earth-mover's distance is the minimum amount of work needed to turn one distribution into the other. The work done to move dirt is the amount of dirt multiplied by the distance it is moved.
Example. Consider the two probability distributions depicted below.
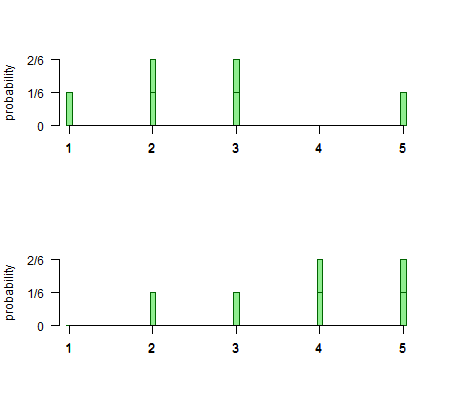
The first one is the distribution of results from throwing a die with six sides labelled 1,2,2,3,3, and 5. The second distribution corresponds to labelling the sides 2,3,4,4,5, and 5.
To turn the first distribution into the second, you could
- Move all the probability (1/6) from 1 to 2;
- Move 2/6 probability from 2 to 4; and
- Move 1/6 probability from 3 to 5.
The work required to do this is (1/6) * (2-1) + (2/6) * (4-2) + (1/6) * (5-3) = 7/6. There are other ways of doing it, but they all require an amount of work at least 7/6. Therefore, the earth-mover's distance between these two distributions is 7/6.
The concept generalizes to probability distributions in more than one dimension, and to continuous distributions of probability, but for this kata we'll limit ourselves to discrete distributions on the line. That is, any distribution can be specified by an array of possible values x and another array px giving the probabilities attached to those values.
The function you need to write takes a probability distribution specified by arrays x and px, and another similarly specified by arrays y and py. It should compute and return the earth-mover's distance between them.
Notes.
1. All the numbers in the test cases are chosen to be representable in binary floating-point with precision to spare (e.g. 1.5 or 0.375, but not 0.1 or 1.7). This means the test suite can (and does) reasonably expect the answers to be computed exactly, without floating-point round-off error.
2. Most of the test cases are small, but there are some larger examples with up to 20000 possible values in each of the distributions -- so you need to consider how your code will handle problems of that size.
Similar Kata:
Stats:
| Created | Feb 26, 2017 |
| Published | Mar 1, 2017 |
| Warriors Trained | 953 |
| Total Skips | 100 |
| Total Code Submissions | 1029 |
| Total Times Completed | 96 |
| C++ Completions | 18 |
| R Completions | 7 |
| Python Completions | 39 |
| Java Completions | 12 |
| JavaScript Completions | 25 |
| C Completions | 14 |
| Total Stars | 38 |
| % of votes with a positive feedback rating | 92% of 38 |
| Total "Very Satisfied" Votes | 33 |
| Total "Somewhat Satisfied" Votes | 4 |
| Total "Not Satisfied" Votes | 1 |
| Total Rank Assessments | 3 |
| Average Assessed Rank | 6 kyu |
| Highest Assessed Rank | 6 kyu |
| Lowest Assessed Rank | 6 kyu |